Advertisements
Advertisements
प्रश्न
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
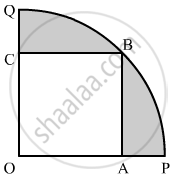
उत्तर
Construction: Join OB
In right triangle AOB
OB2 = OA2 + AB2
= 202 + 202
= 400 + 400
= 800
∴OB2 = 800
Area of the shaded region = Area of quadarant OPBQ - Area of square OABC
`=1/4pi("OB")^2 - ("OA")^2`
`=1/4xx3.14xx800-400`
= 628 - 400
= 228 cm2
Hence, the area of the shaded region is 228 cm2.
APPEARS IN
संबंधित प्रश्न
A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
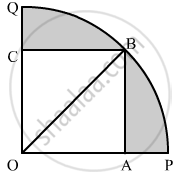
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
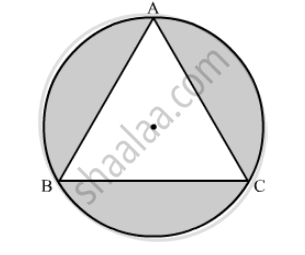
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
The formula used to find the area of the circle is ________ sq.units
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
The radii of the two circles are 4 cm and 3 cm respectively. The diameter of the circle having an area equal to the sum of the areas of the two circles (in cm) is ____________.
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
