Advertisements
Advertisements
प्रश्न
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
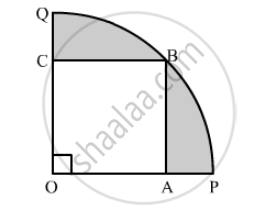
उत्तर
Construction: Join OB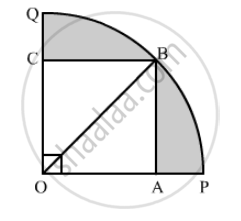
n right triangle AOB
OB2 = OA2 + AB2
= 212 + 212
= 441 + 441
= 882
∴ OB2 = 882
Area of the shaded region = Area of quadrant OPBQ − Area of Square OABC
\[= \frac{1}{4}\pi \left( OB \right)^2 - \left( OA \right)^2 \]
\[ = \frac{1}{4} \times \frac{22}{7} \times 882 - 441\]
\[ = 693 - 441\]
\[ = 252 {cm}^2\]
Hence, the area of the shaded region is 252 cm2.
APPEARS IN
संबंधित प्रश्न
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
A road which is 7 m wide surrounds a circular park whose circumference is 352 m . Find the area of the road .
A square water tank has its side equal to 40 m. There are four semi-circular grassy plots all round it. Find the cost of turfing the plot at Rs. 1.25 per square metre (Take π = 3.14).
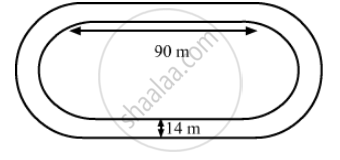
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)

The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
On increasing the diameter of a circle by 40%, its area will be increased by
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
The area of the circle whose diameter is 21 cm is ____________.
