Advertisements
Advertisements
प्रश्न
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
पर्याय
71.5 cm
71.7 cm
72.3 cm
72.7 cm
उत्तर
Area of incircle of equilateral triangle is `154 cm^2`
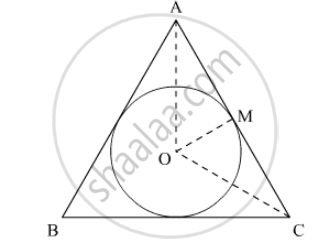
We have to find the perimeter of the triangle. So we will use area to get,
Area of incircle=`154`
`pir^2=154`
`r =sqrt(154/pi) cm`
As triangle is equilateral so,
`∠ OCM=30°`
So,
`tan 30°=r/MC`
`MC=sqrt((154(3))/pi) cm`
So,
`AC=2(MC)`
`=2((sqrt154(3))/pi)cm`
Therefore perimeter of the triangle is,
`= 3(AC)`
`= 6(sqrt462/3.14)`
`=72.7 cm`
APPEARS IN
संबंधित प्रश्न
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

If diameter of a circle is increased by 40%, then its area increase by
In the following figure, the area of the segment PAQ is

What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
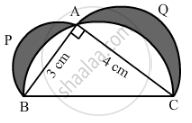
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.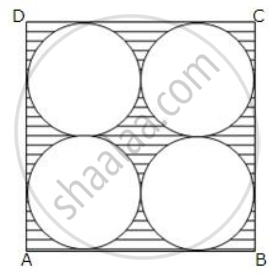
Find the area of the remaining card-board.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
