Advertisements
Advertisements
प्रश्न
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

उत्तर
We will first find the length of the boundary.
Length of the boundary = perimeter of semi-circle with diameter AB + boundary of semi-circle with diameter 7 cm
`"Length of the boundary"=(pixx7+pixx3.5)+pixx1.75+pixx1.75`
`"Length of the boundary"=pi(7+3.5+1.75+1.75)`
`"∴Length of the boundary"=14pi`
`"∴Length of the boundary"=44`
Therefore, length of the boundary is44 cm.
Now we will find the area of the shaded region as shown below,
Area of the shaded region = Area of the semi-circle with AB as a diameter − area of the semi-circle with radius AE − area of the semi-circle with radius BC + area of the semi-circle with diameter 7 cm.
`∴ "Area of the shaded region"=(pixx7xx7)/2-(pixx1.75xx1.75)/2-(pixx1.75xx1.75)/2+(pixx3.5xx3.5)/2`
`∴ "Area of the shaded region"=(49pi)/2-3.0625 pi+12.25/2`
`∴ "Area of the shaded region"=(61.25pi)/2-3.0625pi`
`∴ "Area of the shaded region"=(61.25pu-6.125pi)/2`
`∴ "Area of the shaded region" 55.125xx22/7xx1/2`
`∴ "Area of the shaded region"7.87xx11`
`∴ "Area of the shaded region"=86.625`
Therefore, area of the shaded region is ` 86.625 cm^2`
APPEARS IN
संबंधित प्रश्न
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The circumference of a circle is 100 m. The side of a square inscribed in the circle is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
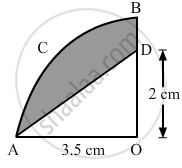
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
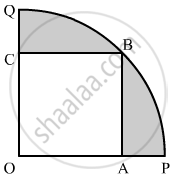
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
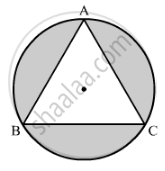
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
Area of a quadrant of a circle of radius 7 cm is ______.
