Advertisements
Advertisements
Question
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

Solution
We will first find the length of the boundary.
Length of the boundary = perimeter of semi-circle with diameter AB + boundary of semi-circle with diameter 7 cm
`"Length of the boundary"=(pixx7+pixx3.5)+pixx1.75+pixx1.75`
`"Length of the boundary"=pi(7+3.5+1.75+1.75)`
`"∴Length of the boundary"=14pi`
`"∴Length of the boundary"=44`
Therefore, length of the boundary is44 cm.
Now we will find the area of the shaded region as shown below,
Area of the shaded region = Area of the semi-circle with AB as a diameter − area of the semi-circle with radius AE − area of the semi-circle with radius BC + area of the semi-circle with diameter 7 cm.
`∴ "Area of the shaded region"=(pixx7xx7)/2-(pixx1.75xx1.75)/2-(pixx1.75xx1.75)/2+(pixx3.5xx3.5)/2`
`∴ "Area of the shaded region"=(49pi)/2-3.0625 pi+12.25/2`
`∴ "Area of the shaded region"=(61.25pi)/2-3.0625pi`
`∴ "Area of the shaded region"=(61.25pu-6.125pi)/2`
`∴ "Area of the shaded region" 55.125xx22/7xx1/2`
`∴ "Area of the shaded region"7.87xx11`
`∴ "Area of the shaded region"=86.625`
Therefore, area of the shaded region is ` 86.625 cm^2`
APPEARS IN
RELATED QUESTIONS
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
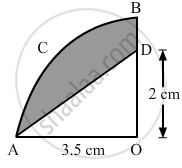
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
The cost of fencing a circular field at the rate of Rs 25 per metre is Rs 5500. The field is to be ploughed at the rate of 50 paise per m2 . Find the cost of ploughing the field. [Take `π =22/7`].
