Advertisements
Advertisements
Question
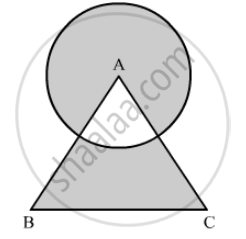
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
Solution
In equilateral traingle all the angles are of 60°
∴ ∠BAC = 60°
Area of the shaded region = (Area of triangle ABC − Area of sector having central angle 60°) + Area of sector having central angle (360° − 60°)
\[= \frac{\sqrt{3}}{4} \left( AB \right)^2 - \frac{60°}{360°}\pi \left( 7 \right)^2 + \frac{300°}{360°}\pi \left( 7 \right)^2 \]
\[ = \frac{\sqrt{3}}{4} \left( 14 \right)^2 - \frac{1}{6} \times \frac{22}{7} \left( 7 \right)^2 + \frac{5}{6} \times \frac{22}{7} \left( 7 \right)^2 \]
\[ = 84 . 77 - 25 . 67 + 128 . 35\]
\[ = 187 . 45 {cm}^2\]
Hence, the area of shaded region is 187.45 cm2
APPEARS IN
RELATED QUESTIONS
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
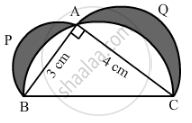
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
Calculate the area of the shotput circle whose radius is 2.135 m.
