Advertisements
Advertisements
प्रश्न
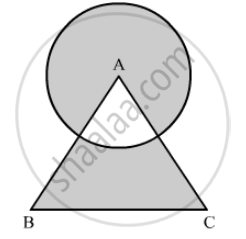
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
उत्तर
In equilateral traingle all the angles are of 60°
∴ ∠BAC = 60°
Area of the shaded region = (Area of triangle ABC − Area of sector having central angle 60°) + Area of sector having central angle (360° − 60°)
\[= \frac{\sqrt{3}}{4} \left( AB \right)^2 - \frac{60°}{360°}\pi \left( 7 \right)^2 + \frac{300°}{360°}\pi \left( 7 \right)^2 \]
\[ = \frac{\sqrt{3}}{4} \left( 14 \right)^2 - \frac{1}{6} \times \frac{22}{7} \left( 7 \right)^2 + \frac{5}{6} \times \frac{22}{7} \left( 7 \right)^2 \]
\[ = 84 . 77 - 25 . 67 + 128 . 35\]
\[ = 187 . 45 {cm}^2\]
Hence, the area of shaded region is 187.45 cm2
APPEARS IN
संबंधित प्रश्न
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

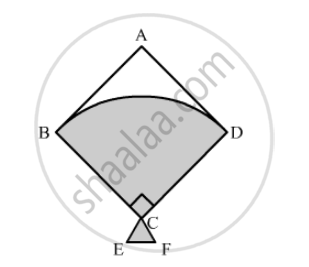
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
In the following figure, the area of the segment PAQ is

In the following figure, the area of the shaded region is
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
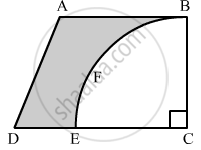
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
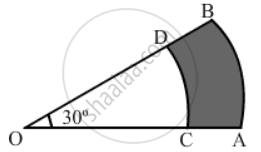
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
