Advertisements
Advertisements
प्रश्न
In the following figure, the area of the segment PAQ is

विकल्प
\[\frac{a^2}{4}\left( \pi + 2 \right)\]
\[\frac{a^2}{4}\left( \pi - 2 \right)\]
\[\frac{a^2}{4}\left( \pi - 1 \right)\]
\[\frac{a^2}{4}\left( \pi + 1 \right)\]
उत्तर
We have to find area of segment PAQ.
Area of the PAQ segment=` (piθ/360-sin θ/2 cos θ/2)r^2`
We know that. `θ=90°`
Substituting the values we get,
Area of the PAQ segment = `((pixx90)/360-sin 45 cos 45)a^2`
`∴" Area of the PAQ segment" =(pi/4-sin 45 cos 45)a^2`
Substituting sin 45=1/sqrt2 and `cos 45=1/sqrt2` and `cos 45=1/sqrt2` we get
`"Area of the PAQ segment"=(pi/4-1/sqrt2xx1/sqrt2)a^2`
∴`" Area of the PAQ segment" =( pi/4-1/2 ) a^2`
Now we will make the denominator same.
∴`"Area of the PAQ segment" =(pi/4-2/4)a^2`
∴`"Area of the PAQ segment"((pi-2)/4)a^2`
∴`"Area of the PAQ segment"=(pi-2)a^2/4`
∴`"Area of the PAQ segment"= a^2/4(pi-2)`
Therefore, area of the segment PAQ is `a^2/4 (pi-2)`
APPEARS IN
संबंधित प्रश्न
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

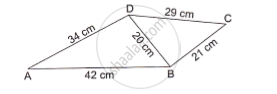
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
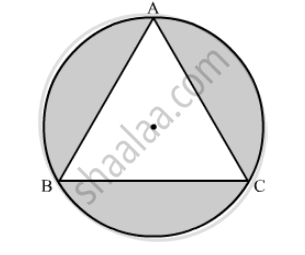
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

If the circumference of a circle increases from 4π to 8π, then its area is
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
The length of an arc of a circle, subtending an angle of 54° at the centre, is 16.5 cm. Calculate the radius, circumference and area of the circle.
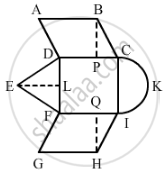
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
The circumference of a circular table is 88 m. Find its area.
