Question

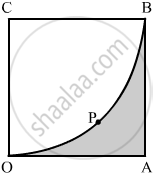
In the following figure, the area of the segment PAQ is 

 

पर्याय

• \[\frac{a^2}{4}\left( \pi + 2 \right)\]

• \[\frac{a^2}{4}\left( \pi - 2 \right)\]

• \[\frac{a^2}{4}\left( \pi - 1 \right)\]

• \[\frac{a^2}{4}\left( \pi + 1 \right)\] 

Answer 1

We have to find area of segment PAQ. 

Area of the PAQ segment=` (piθ/360-sin   θ/2 cos  θ/2)r^2`

We know that. `θ=90°`

Substituting the values we get,

Area of the PAQ segment = `((pixx90)/360-sin 45 cos 45)a^2`

`∴" Area of the PAQ segment" =(pi/4-sin 45 cos 45)a^2`

Substituting sin 45=1/sqrt2 and `cos 45=1/sqrt2` and `cos 45=1/sqrt2` we get

`"Area of the PAQ segment"=(pi/4-1/sqrt2xx1/sqrt2)a^2`

∴`" Area of the PAQ segment" =( pi/4-1/2 ) a^2`

Now we will make the denominator same.

∴`"Area of the PAQ segment" =(pi/4-2/4)a^2` 

∴`"Area of the PAQ segment"((pi-2)/4)a^2`

∴`"Area of the PAQ segment"=(pi-2)a^2/4`

∴`"Area of the PAQ segment"= a^2/4(pi-2)`

Therefore, area of the segment PAQ is `a^2/4 (pi-2)`