Advertisements
Advertisements
प्रश्न
A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is `12m^2` find its width.
उत्तर
Let the width of the border be x m.
The length and breadth of the carpet are 8 m and 5 m, respectively. Area of the carpet=`8xx5=40m^2`
Length of the carpet without border=`(8-2x)`
Breadth of carpet without border=`(5-2x)`
Area of the border`12m^2`
Area of the carpet without border=`(8-2x)(5-2x)`
Thus, we have:
`12=40-[(8-2x)(5-2x)]`
⇒ `12=40-(40-26x+4x^2)`
⇒ `12=26x-4x^2`
⇒ `26x-4x^2=12`
⇒`4x^2-26x+12=0`
⇒`2x^2-13x+6=0`
⇒`(2x-1)(x-6)=0`
⇒`2x-1=0 and x-6=0`
⇒`x=1/2 and x=6`
Because the border cannot be wider than the entire carpet, the width of the carpet is `1/2 m `
i.e. `50 cm`
APPEARS IN
संबंधित प्रश्न
A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
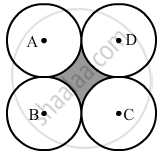
Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
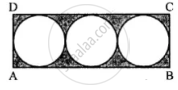
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
