Advertisements
Advertisements
प्रश्न
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
उत्तर
The length and breadth of the lawn are 80 m and 64 m, respectively. The layout of the roads is shown in the figure below:
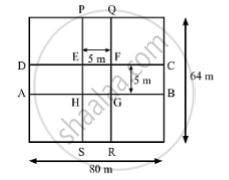
Area of the road ABCD =`80xx5=400m^2`
Area of the road PQRS=`64xx5=320 m^2`
Clearly, the area EFGH is common in both the roads
Area EFGH =`5xx5=25m^2`
Area of the roads = `400+300-25`
=` 695m^2`
Given:
Cost of gravelling `1m^2` area
Cost of gravelling `695m^2` area =`695xx40`
=Rs `27,800`
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
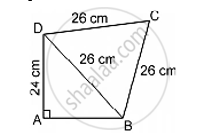
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
The perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
