Advertisements
Advertisements
प्रश्न
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
पर्याय
10 \[\sqrt{5}\]
10\[\sqrt{3}\]cm
10\[\sqrt{5}\]
10\[\sqrt{2}\]
उत्तर
The circle can be divided into four parts of equal area by drawing three concentric circles inside it as,

It is given that OB = 20 cm. Let OA = x.
Since the circle is divided into four parts of equal area by the three concentric circles, we have,
Area of the fourth region `=1/4xx`Area of the given circle
`pixx(20^2-x^2)=1/4xxpixx20^2`
`400-x^2=100`
`x^2=300`
`x-10sqrt3 cm`
APPEARS IN
संबंधित प्रश्न
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

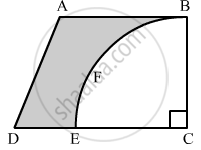
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
The area of a circle is 98.56 cm2. Find its circumference.
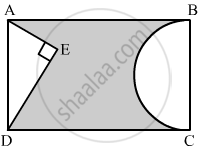
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).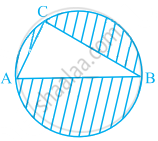
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
Find the area of the shaded region: