Advertisements
Advertisements
प्रश्न
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
विकल्प
10 \[\sqrt{5}\]
10\[\sqrt{3}\]cm
10\[\sqrt{5}\]
10\[\sqrt{2}\]
उत्तर
The circle can be divided into four parts of equal area by drawing three concentric circles inside it as,

It is given that OB = 20 cm. Let OA = x.
Since the circle is divided into four parts of equal area by the three concentric circles, we have,
Area of the fourth region `=1/4xx`Area of the given circle
`pixx(20^2-x^2)=1/4xxpixx20^2`
`400-x^2=100`
`x^2=300`
`x-10sqrt3 cm`
APPEARS IN
संबंधित प्रश्न
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
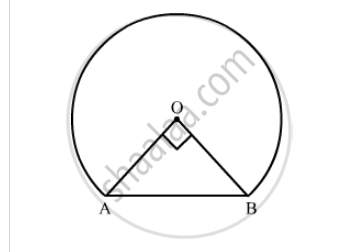
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
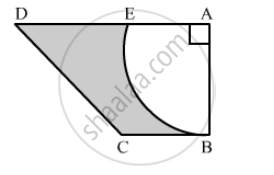
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
A circular disc of radius 6 cm is divided into three sectors with central angles 90°,120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Find the area of the dining table whose diameter is 105 cm
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).