Advertisements
Advertisements
प्रश्न
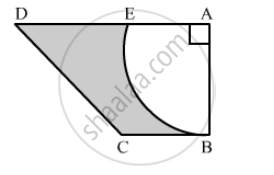
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
उत्तर
Area of trapezium =\[\left( 3\pi + 2 \right) m^2\]
\[\Rightarrow 24 . 5 = \frac{1}{2}\left( 10 + 4 \right) \times AB\]
\[ \Rightarrow AB = 3 . 5 cm\]
Area of shaded region = Area of trapezium ABCD − Area of quadrant ABE
\[= 24 . 5 - \frac{1}{4} \times \frac{22}{7} \times \left( 3 . 5 \right)^2 \]
\[ = 24 . 5 - 9 . 625\]
\[ = 14 . 875 {cm}^2\]
Hence, the area of shaded region is 14.875 cm2
APPEARS IN
संबंधित प्रश्न
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
The area of the circle that can be inscribed in a square of side 6 cm is ______.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
