Advertisements
Advertisements
प्रश्न
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
विकल्प
2800
4000
5500
7000
उत्तर
We have given the radius of the wheel that is 0.25 cm.
We know that distance covered by the wheel in one revolution=`" Distance moved"/"Number of revolutions"`
Distance covered by the wheel in one revolution is equal to the circumference of the wheel.
`2pi r="Distance moved"/"Number of revolutions"......(1)`
Distance moved is given as 11 km so we will first convert it to m.
∴ 11 km = 11000 m
Now we will substitute the values in equation (1),
`2xxpixx0.25=11000/"Number of revalution"`
Now we will substitute pi=`22/7`
`2xx22/7xx0.25=11000/"Number of revolutions"`
Simplifying equation (1) we get,
`∴" Number of revolutions"=(11000xx7)/(2xx22xx0.25)`
`∴" Number of revolutions"=(11000xx7)/(22xx0.5)`
`∴" Number of revolutions"=(1000xx7)/(2xx0.5)`
`∴" Number of revolutions"=7000/1`
`∴" Number of revolutions"=7000`
Therefore, it will make `7000` revolutions to travel a distance of 11 km.
APPEARS IN
संबंधित प्रश्न
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
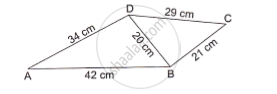
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
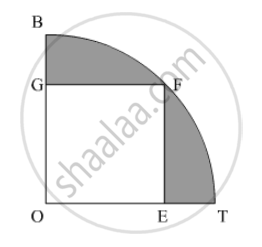
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
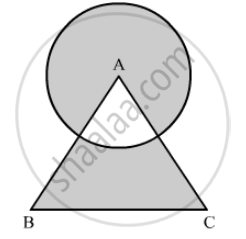
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
If diameter of a circle is increased by 40%, then its area increase by
The length of an arc of a circle, subtending an angle of 54° at the centre, is 16.5 cm. Calculate the radius, circumference and area of the circle.
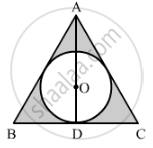
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
