Advertisements
Advertisements
प्रश्न
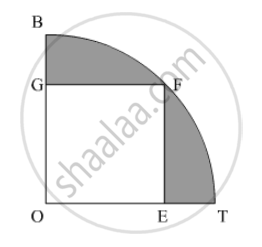
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
उत्तर
We have to find the area of the shaded portion. We have, `OE=20cm`and OEFG is a square.
Use Pythagoras theorem to find OF as,
`OF=(sqrt((20)^2+(20)^2))cm`
`= 20sqrt2 cm`
So, radius of the circle,
`OF=20sqrt2 cm`
Therefore area of the shaded region,
`"Area of the shade region=(Area of quadrant of circle)-(Area of square)"`
So,
Area of the shaded region =`(pi(OF)^2)/4-(OE)^2`
`(22/7)((20sqrt2^2)/4)-(20)^2`
=`628-400`
`=228 cm^2`
APPEARS IN
संबंधित प्रश्न
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is `12m^2` find its width.
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
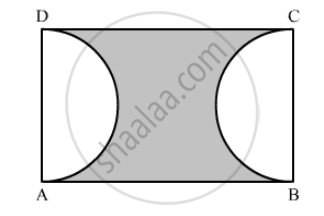
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
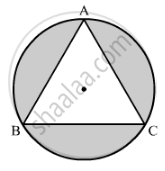
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
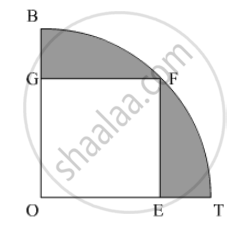
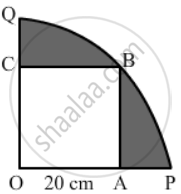
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
