Advertisements
Advertisements
प्रश्न
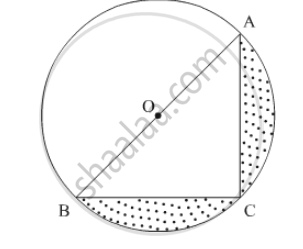
Find the area of the shaded region in the following figure, if AC = 24 cm, BC = 10 cm and O is the centre of the circle. (Use π = 3.14)
उत्तर
It is given a triangle ABC is cut from a circle.
`AC=24 cm `
`BC=10 cm`
`"Area of ΔABC=1/2 ACxxBC"`
` = 1/2xx24xx10`
`=120 cm^2`

In ΔABC,
`∠ACB`, Since any angle inscribed in semicircle is always right angle.
By applying Pythagoras theorem,
`AB^2=AC^2+BC^2`
`=24xx24+10xx10`
`=576++100`
`=676 cm^2`
`OA=AB/2`
`=26/2 cm`
`=13 cm`
We know that the area A of circle of radius r is
`A=pi r^2
`Substituting the value of radius r,
`A=3.14xx13xx13`
`= 530.66 cm^2`
Area of semicircle=`1/2 pir^2`
` =530.66/2 cm^2`
` =265.33 cm^2`
`"Area of shadded region=Area of semicircle-Area of triangle" `
`=530.66-265.33-120`
`= 145.33 cm^2`
APPEARS IN
संबंधित प्रश्न
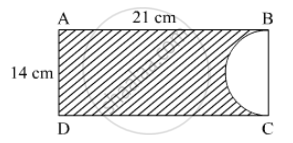
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
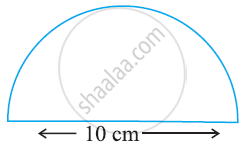
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
A path of width 3.5 m runs around a semi-circular grassy plot whose perimeter is 72 m . Find the area of the path .
`("Use" pi= 22/7) `
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
The perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
