Advertisements
Advertisements
Question
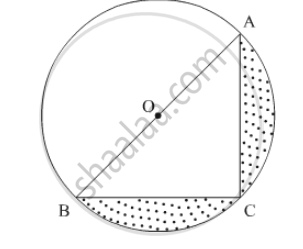
Find the area of the shaded region in the following figure, if AC = 24 cm, BC = 10 cm and O is the centre of the circle. (Use π = 3.14)
Solution
It is given a triangle ABC is cut from a circle.
`AC=24 cm `
`BC=10 cm`
`"Area of ΔABC=1/2 ACxxBC"`
` = 1/2xx24xx10`
`=120 cm^2`

In ΔABC,
`∠ACB`, Since any angle inscribed in semicircle is always right angle.
By applying Pythagoras theorem,
`AB^2=AC^2+BC^2`
`=24xx24+10xx10`
`=576++100`
`=676 cm^2`
`OA=AB/2`
`=26/2 cm`
`=13 cm`
We know that the area A of circle of radius r is
`A=pi r^2
`Substituting the value of radius r,
`A=3.14xx13xx13`
`= 530.66 cm^2`
Area of semicircle=`1/2 pir^2`
` =530.66/2 cm^2`
` =265.33 cm^2`
`"Area of shadded region=Area of semicircle-Area of triangle" `
`=530.66-265.33-120`
`= 145.33 cm^2`
APPEARS IN
RELATED QUESTIONS
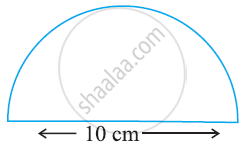
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
The area of a square filed is 8 hectares. How long would a man take to cross it diagonally by walking at the rate of 4 km per hour?
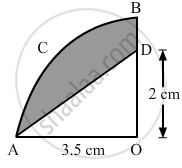
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
If diameter of a circle is increased by 40%, then its area increase by
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
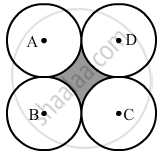
Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
The area of the circle is 154 cm2. The radius of the circle is ______.
The radii of the two circles are 4 cm and 3 cm respectively. The diameter of the circle having an area equal to the sum of the areas of the two circles (in cm) is ____________.
