Advertisements
Advertisements
Question
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
Options
34
26
17
14
Solution
Let the diameter of the larger circle be d
Now, Area of larger circle = Area of circle having diameter 10 cm + Area of circle having diameter 24 cm
\[\Rightarrow \pi \left( \frac{d}{2} \right)^2 = \pi \left( \frac{10}{2} \right)^2 + \pi \left( \frac{24}{2} \right)^2 \]
\[ \Rightarrow \left( \frac{d}{2} \right)^2 = \left( 5 \right)^2 + \left( 12 \right)^2\]
\[ \Rightarrow \left( \frac{d}{2} \right)^2 = {13}^2 \]
\[ \Rightarrow \frac{d}{2} = 13\]
\[ \Rightarrow d = 26 cm\]
APPEARS IN
RELATED QUESTIONS
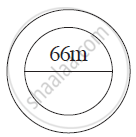
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
The perimeter of the sector OAB shown in the following figure, is

If the difference between the circumference and radius of a circle is 37 cm, then its area is
If diameter of a circle is increased by 40%, then its area increase by
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


