Advertisements
Advertisements
Questions
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
The minute hand of a clock is 14 cm long; Find the area on the face of the clock described by the minute hand in 5 minutes.
Solution
Angle make by the minute hand in 1 minute = 6∘
Angle make by the minute hand in 5 minute = 5 ⨯ 6∘ = 30∘
The area of the sector having a central angle is given by
= `(30°)/(360°) xx pi xx (14)^2`
`=1/12 xx22/7 xx (14)^2`
`=51.33 cm^2`
Hence, the area swept by minute hand in 5 minutes is 51.33 cm2
RELATED QUESTIONS
Find the area of the following circle, given that radius = 14 mm (take `pi = 22/7`).
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
A rectangular park is 100 m by 50 m. It is surrounding by semi-circular flower beds all round. Find the cost of levelling the semi-circular flower beds at 60 paise per square metre (use π = 3.14).
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be ______.
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is ______.
Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.
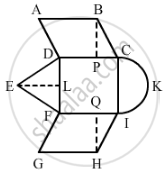
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
