Advertisements
Advertisements
Question
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
Solution
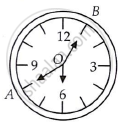
We know that, in 60 mins, minute hand revolving = 360°
In 1 min, minute hand revolving = `360^circ/60^circ`
∴ In (6 : 05 am to 6 : 40 am) = 35 mins,
minute hand revolving = `360^circ/60 xx 35` = (6 × 35)°
Given that, length of minute hand (r) = 5 cm
∴ Area of sector AOBA with angle ∠O
= `(π"r"^2)/360^circ xx ∠"O"`
= `22/7 xx (5)^2/360^circ xx (6 xx 35)^circ`
= `22/7 xx (5 xx 5)/360^circ xx (6 xx 35)^circ`
= `(22 xx 5 xx 5 xx 5)/60^circ`
= `(22 xx 5 xx 5)/12`
= `(11 xx 5 xx 5)/6`
= `275/6`
= `45 5/6 "cm"^2`
Hence, the required area swept by the minute hand is `45 5/6 "cm"^2`.
APPEARS IN
RELATED QUESTIONS
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

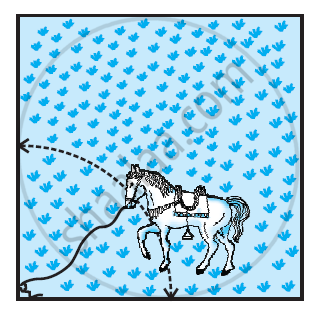
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
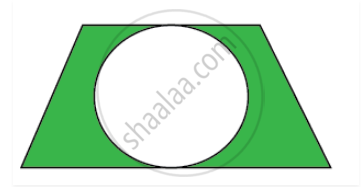
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
