Advertisements
Advertisements
Question
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Solution
Given that, a triangular field with the three corners of the field a cow, a buffalo and a horse are tied separately with ropes.
So, each animal grazed the field in each corner of triangular field as a sectorial form.
Given, radius of each sector (r) = 7 m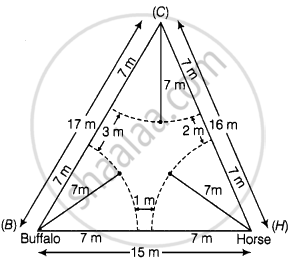
Now, area of sector with ∠C
= `(∠"C")/360^circ xx pi"r"^2`
= `(∠"C")/360^circ xx pi xx (7)^2"m"^2`
Area of the sector with ∠B
= `(∠"B")/360^circ xx pi"r"^2`
= `(∠"B")/360^circ xx pi xx (7)^2"m"^2`
And area of the sector with ∠H
= `(∠"H")/360^circ xx pi"r"^2`
= `(∠"H")/360^circ xx pi xx (7)^2"m"^2`
Therefore, sum of the area (in cm2) of the three sectors
= `(∠"C")/360^circ xx pi xx (7)^2 + (∠"B")/360^circ xx pi xx (7)^2 + (∠"H")/360^circ xx pi xx (7)^2`
= `((∠"C" + ∠"B" + ∠"H"))/360^circ xx pi xx 49`
= `180^circ/360^circ xx 22/7 xx 49`
= 11 × 7
= 77 cm2
Given that, sides of triangle are a = 15, b = 16 and c = 17
Now, semi-perimeter of triangle,
s = `("a" + "b" + "c")/2`
⇒ `(15 + 16 + 17)/2 = 48/2` = 24
∴ Area of triangular field
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))` ...[By Heron's formula]
= `sqrt(24 * 9 * 8* 7)`
= `sqrt(64 * 9 * 21)`
= `8 xx 3sqrt(21)`
= `24sqrt(21) "m"^2`
So, area of the field which cannot be grazed by the three animals
= Area of triangular field – Area of each sectorial field
= `24sqrt(21) - 77 "m"^2`
Hence, the required area of the field which cannot be grazed by the three animals is `(24sqrt(21) - 77) "m"^2`.
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
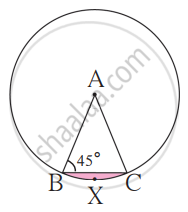
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
