Advertisements
Advertisements
प्रश्न
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
उत्तर
Given that, a triangular field with the three corners of the field a cow, a buffalo and a horse are tied separately with ropes.
So, each animal grazed the field in each corner of triangular field as a sectorial form.
Given, radius of each sector (r) = 7 m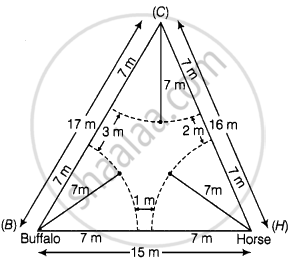
Now, area of sector with ∠C
= `(∠"C")/360^circ xx pi"r"^2`
= `(∠"C")/360^circ xx pi xx (7)^2"m"^2`
Area of the sector with ∠B
= `(∠"B")/360^circ xx pi"r"^2`
= `(∠"B")/360^circ xx pi xx (7)^2"m"^2`
And area of the sector with ∠H
= `(∠"H")/360^circ xx pi"r"^2`
= `(∠"H")/360^circ xx pi xx (7)^2"m"^2`
Therefore, sum of the area (in cm2) of the three sectors
= `(∠"C")/360^circ xx pi xx (7)^2 + (∠"B")/360^circ xx pi xx (7)^2 + (∠"H")/360^circ xx pi xx (7)^2`
= `((∠"C" + ∠"B" + ∠"H"))/360^circ xx pi xx 49`
= `180^circ/360^circ xx 22/7 xx 49`
= 11 × 7
= 77 cm2
Given that, sides of triangle are a = 15, b = 16 and c = 17
Now, semi-perimeter of triangle,
s = `("a" + "b" + "c")/2`
⇒ `(15 + 16 + 17)/2 = 48/2` = 24
∴ Area of triangular field
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))` ...[By Heron's formula]
= `sqrt(24 * 9 * 8* 7)`
= `sqrt(64 * 9 * 21)`
= `8 xx 3sqrt(21)`
= `24sqrt(21) "m"^2`
So, area of the field which cannot be grazed by the three animals
= Area of triangular field – Area of each sectorial field
= `24sqrt(21) - 77 "m"^2`
Hence, the required area of the field which cannot be grazed by the three animals is `(24sqrt(21) - 77) "m"^2`.
संबंधित प्रश्न
An umbrella has 8 ribs which are equally spaced. Assuming umbrella to be a flat circle of radius 45 cm. Find the area between the two consecutive ribs of the umbrella.
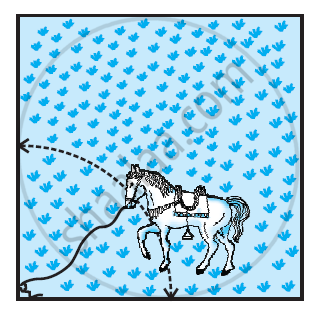
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
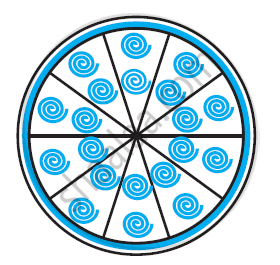
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
