Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The area of sector of circle of radius 5cm is 5ЁЭЬЛ cm2. Find the angle contained by the sector.
рдЙрддреНрддрд░
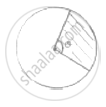
Area of sector = 5ЁЭЬЛ cm2.
Radius (r) = 5cm
Let ЁЭЬГ = angle subtended at centre area of sector =`theta/360^@× pir^2`
=`theta/360× pi × 5 × 5 =(5pitheta)/72^@`
=`(5pitheta)/72^@`= 5ЁЭЬЛ
⇒ ЁЭЬГ = 72°
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
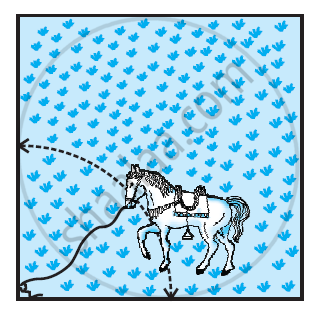
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
