Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The area of sector of circle of radius 2cm is ЁЭЬЛcm2. Find the angle contained by the sector.
рдЙрддреНрддрд░
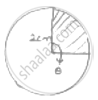
Area of sector = ЁЭЬЛ ЁЭСРЁЭСЪ2
Radius of circle = 2ЁЭСРЁЭСЪ
Let ЁЭЬГ = angle subtended by arc at centre
Area of sector =`theta/360^@× pir^2`
=`theta/360^@× pi× 2 × 2`
=`(pitheta)/90^@`
`(pitheta)/90^@`= ЁЭЬЛ ⇒ ЁЭЬГ = 90°
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60╦Ъ. Also find the area of the corresponding major segment.[use π=22/7]
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
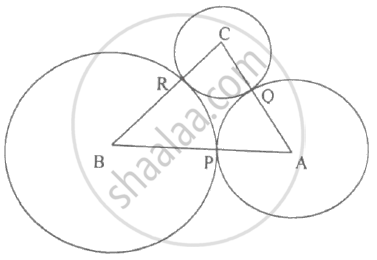
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.
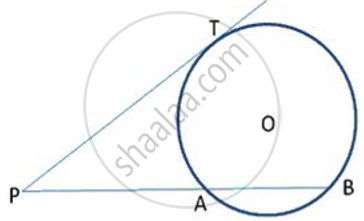
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
