Advertisements
Advertisements
प्रश्न
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

उत्तर
∠ AOB = q
Reflex ∠ AOB = 360 - q
Since arc AB subtends reflex ∠ AOB = (360 - q)° at the centre and ∠ ACB on the remaining part of the circle .
∴ ∠ ACB = `1/2` (reflex ∠ AOB)
If OACB is a parallelogram
∠ AOB = ∠ ACB
q = p
360 - 2p = p
3p = 360
p = 120°
APPEARS IN
संबंधित प्रश्न
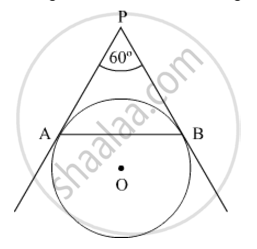
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
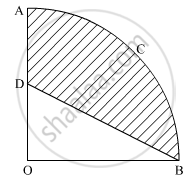
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

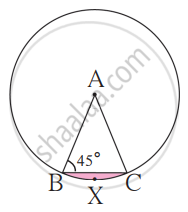
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

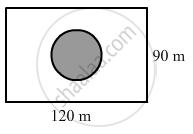
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
