Advertisements
Advertisements
प्रश्न
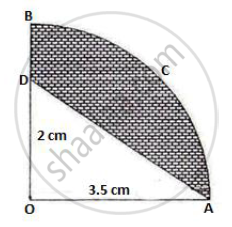
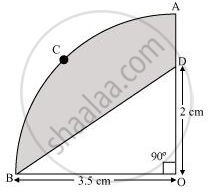
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
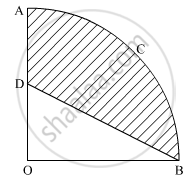
In the figure alongside, OACB is a quadrant of a circle. The radius OA = 3.5 cm and OD = 2 cm. Calculate the area of the shaded portion (Take Π = 22/7)
उत्तर १
Since OACB is a quadrant, it will subtend 90° angle at O.
Area of quadrant OACB
`= 90^@/360^@ xx pir^2`
`=1/4 xx 22/7 xx (3.5)^2 = 1/4 xx 22/7 xx(7/2)^2`
`= (11xx7xx7)/(2xx 7xx 2xx2) = 77/8 cm^2`
Area of ΔOBD
`= 1/2 xx OB xx OD`
`= 1/2 xx 3.5 xx 2`
`= 1/2 xx 7/2 xx 2`
`= 7/2 "cm"^2`
Area of the shaded region
= Area of quadrant OACB − Area of ΔOBD
`= 77/8 - 7/2`
`= (77 - 28)/8`
= `49/8 "cm"^2`
उत्तर २
Area of the quadrant OACB = `1/4 xx pir^2`
`= 1/4 xx 22/7 xx 3.5 xx 3.5`
`= 9.625 cm^2`
Area of the triangle OAD = `1/2 xx base xx height = 1/2 cc 3.5 xx 2 = 3.5 cm^2`
Shaded Area = Area of quadrant OACB – area of triangle OAD
` = 9.625 - 3.5 cm^2`
`= 6.125 cm^2`
APPEARS IN
संबंधित प्रश्न
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
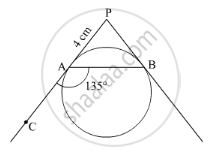
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
