Advertisements
Advertisements
Questions
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
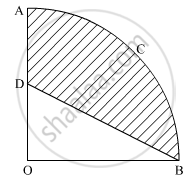
In the figure alongside, OACB is a quadrant of a circle. The radius OA = 3.5 cm and OD = 2 cm. Calculate the area of the shaded portion (Take Π = 22/7)
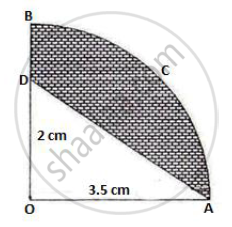
Solution 1
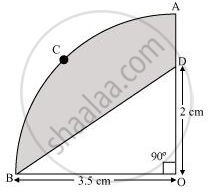
Since OACB is a quadrant, it will subtend 90° angle at O.
Area of quadrant OACB
`= 90^@/360^@ xx pir^2`
`=1/4 xx 22/7 xx (3.5)^2 = 1/4 xx 22/7 xx(7/2)^2`
`= (11xx7xx7)/(2xx 7xx 2xx2) = 77/8 cm^2`
Area of ΔOBD
`= 1/2 xx OB xx OD`
`= 1/2 xx 3.5 xx 2`
`= 1/2 xx 7/2 xx 2`
`= 7/2 "cm"^2`
Area of the shaded region
= Area of quadrant OACB − Area of ΔOBD
`= 77/8 - 7/2`
`= (77 - 28)/8`
= `49/8 "cm"^2`
Solution 2
Area of the quadrant OACB = `1/4 xx pir^2`
`= 1/4 xx 22/7 xx 3.5 xx 3.5`
`= 9.625 cm^2`
Area of the triangle OAD = `1/2 xx base xx height = 1/2 cc 3.5 xx 2 = 3.5 cm^2`
Shaded Area = Area of quadrant OACB – area of triangle OAD
` = 9.625 - 3.5 cm^2`
`= 6.125 cm^2`
APPEARS IN
RELATED QUESTIONS
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.

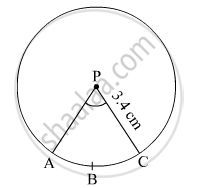
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
