Advertisements
Advertisements
Question
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
Solution
Given:
Area of the sector = 63 cm2
Radius = 10.5 cm
Now,
Area of the sector`=(pi"r"^2theta)/360`
`=> 69.3 = 22/7xx10.5xx10.5xxtheta/360`
`=> theta = (69.3xx7xx360)/(22xx10.5xx10.5)`
⇒ θ = 72°
∴ Central angle of the sector = 72°
APPEARS IN
RELATED QUESTIONS
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
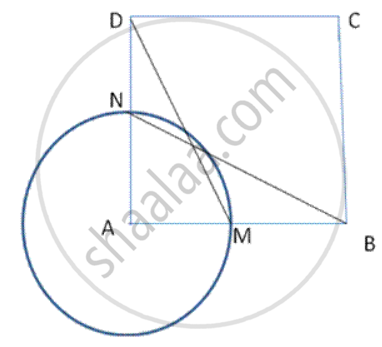
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).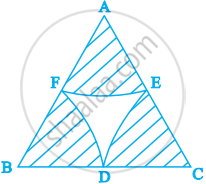
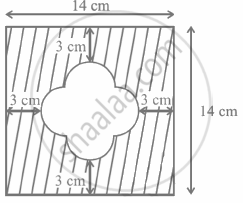
Find the area of the unshaded region shown in the given figure.