Topics
Number Systems
Real Numbers
Algebra
Polynomials
Pair of Linear Equations in Two Variables
- Introduction to linear equations in two variables
- Graphical Method
- Substitution Method
- Elimination Method
- Cross - Multiplication Method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Consistency of Pair of Linear Equations
- Inconsistency of Pair of Linear Equations
- Algebraic Conditions for Number of Solutions
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Relation Between Co-efficient
Quadratic Equations
- Quadratic Equations
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Nature of Roots of a Quadratic Equation
- Relationship Between Discriminant and Nature of Roots
- Situational Problems Based on Quadratic Equations Related to Day to Day Activities to Be Incorporated
- Application of Quadratic Equation
Arithmetic Progressions
Coordinate Geometry
Lines (In Two-dimensions)
Constructions
- Division of a Line Segment
- Construction of Tangents to a Circle
- Constructions Examples and Solutions
Geometry
Triangles
- Similar Figures
- Similarity of Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Right-angled Triangles and Pythagoras Property
- Similarity of Triangles
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Triangles Examples and Solutions
- Concept of Angle Bisector
- Similarity of Triangles
- Ratio of Sides of Triangle
Circles
Trigonometry
Introduction to Trigonometry
- Trigonometry
- Trigonometry
- Trigonometric Ratios
- Trigonometric Ratios and Its Reciprocal
- Trigonometric Ratios of Some Special Angles
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
- Proof of Existence
- Relationships Between the Ratios
Trigonometric Identities
Some Applications of Trigonometry
Mensuration
Areas Related to Circles
- Perimeter and Area of a Circle - A Review
- Areas of Sector and Segment of a Circle
- Areas of Combinations of Plane Figures
- Circumference of a Circle
- Area of Circle
Surface Areas and Volumes
- Surface Area of a Combination of Solids
- Volume of a Combination of Solids
- Conversion of Solid from One Shape to Another
- Frustum of a Cone
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Different Combination of Solid Figures
- Surface Area and Volume of Three Dimensional Figures
Statistics and Probability
Statistics
Probability
Internal Assessment
- Area of the Sector and Circular Segment
- Length of an Arc
Notes
1) Sector- The portion (or part) of the circular region enclosed by two radii and the corresponding arc is called a sector of the circle.

Here, OAPB is the minor sector and OAQB is the major sector.
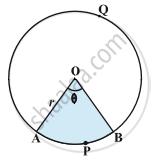
Let OAPB be a sector of a circle with centre O and radius r. Let the degree measure of ∠AOB be θ.
Now, area of a circle= `πr^2`
We can consider this circular region to be a sector forming an angle of 360° at the centre O.
When angle at the centre is 360, area of the sector= `πr^2`
when angle at the centre is 1, area of the sector= `(πr^2)/360`
So, when angle at the centre is θ.
area of the sector= `(πr^2)/360 xx θ`
area of the sector= `θ/360 xx πr^2`
2) Segment- The potion (or part) of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.
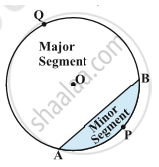
arc APB is the minor segment and arc AQB is the major segment.
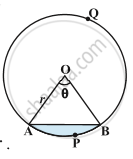
Here, in a circle with centre O and radius r, You can see that:
Area of the segment APB = Area of the sector OAPB- Area of ΔOAB
`"Area" "of" "the" "segment" "APB" =θ/360 xx πr^2- "Area" "of" "ΔOAB"`