Topics
Number Systems
Real Numbers
Algebra
Polynomials
Pair of Linear Equations in Two Variables
- Introduction to linear equations in two variables
- Graphical Method
- Substitution Method
- Elimination Method
- Cross - Multiplication Method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Consistency of Pair of Linear Equations
- Inconsistency of Pair of Linear Equations
- Algebraic Conditions for Number of Solutions
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Relation Between Co-efficient
Quadratic Equations
- Quadratic Equations
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Nature of Roots of a Quadratic Equation
- Relationship Between Discriminant and Nature of Roots
- Situational Problems Based on Quadratic Equations Related to Day to Day Activities to Be Incorporated
- Application of Quadratic Equation
Arithmetic Progressions
Coordinate Geometry
Lines (In Two-dimensions)
Constructions
- Division of a Line Segment
- Construction of Tangents to a Circle
- Constructions Examples and Solutions
Geometry
Triangles
- Similar Figures
- Similarity of Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Right-angled Triangles and Pythagoras Property
- Similarity of Triangles
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Triangles Examples and Solutions
- Concept of Angle Bisector
- Similarity of Triangles
- Ratio of Sides of Triangle
Circles
Trigonometry
Introduction to Trigonometry
- Trigonometry
- Trigonometry
- Trigonometric Ratios
- Trigonometric Ratios and Its Reciprocal
- Trigonometric Ratios of Some Special Angles
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
- Proof of Existence
- Relationships Between the Ratios
Trigonometric Identities
Some Applications of Trigonometry
Mensuration
Areas Related to Circles
- Perimeter and Area of a Circle - A Review
- Areas of Sector and Segment of a Circle
- Areas of Combinations of Plane Figures
- Circumference of a Circle
- Area of Circle
Surface Areas and Volumes
- Surface Area of a Combination of Solids
- Volume of a Combination of Solids
- Conversion of Solid from One Shape to Another
- Frustum of a Cone
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Different Combination of Solid Figures
- Surface Area and Volume of Three Dimensional Figures
Statistics and Probability
Statistics
Probability
Internal Assessment
- Theorem: When two triangles are similar, the ratio of areas of those triangles is equal to the ratio of the squares of their corresponding sides.
Theorem
Theorem1: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
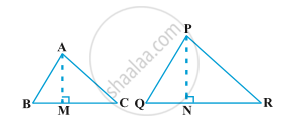
Given: ∆ABC ∼ ∆PQR
Construction: Draw AM ⊥ BC and PN ⊥ QR
To prove: `"ar∆ABC"/"ar∆PQR" = ("AB"/"PQ")^2= ("BC"/"QR")^2= ("AC"/"PR")^2`
Proof: ∆ABC ∼ ∆PQR (Given)
`"AB"/"PQ"= "BC"/"QR" = "AC"/"PR"` (Corresponding parts of Congruent triangles) ...eq1
and ∠B= ∠Q (Corresponding parts of Congruent triangles)
Now, `"ar(∆ABC)"= 1/2 × "BC" × "AM"`
`"ar(∆PQR)"= 1/2 × "QR" × "PN"`
`"ar(∆ABC)"/"ar(∆PQR)"= (1/2 xx "BC" xx "AM")/(1/2 xx "QR" xx "PN")`
`"ar(∆ABC)"/"ar(∆PQR)"`= `"BC"/"QR"×"AM"/"PN"` .......eq2
Again, In ∆ABM and ∆PQN
∠AMB = ∠PNQ = 90°
∠B= ∠Q (Corresponding parts of Congruent triangles)
∆ABM ∼ ∆PQN
So, `"AB"/"PQ"= "AM"/"PN"` (Corresponding parts of Congruent triangles) .....eq3
From eq2 and eq3
`"ar(∆ABC)"/"ar(∆PQR)"= "BC"/"QR"×"AB"/"PQ"` ......eq4
From eq1 and eq4
`"ar(∆ABC)"/"ar(∆PQR)"= "BC"/"QR" × "BC"/"QR"`
`"ar(∆ABC)"/"ar(∆PQR)"= ("BC"/"QR")^2` .........eq5
From eq1 and eq5
`"ar(∆ABC)"/"ar(∆PQR)"= ("AB"/"PQ")^2 = ("BC"/"QR")^2 = ("AC"/"PR")^2`
Hence proved.