Topics
Number Systems
Real Numbers
Algebra
Polynomials
Pair of Linear Equations in Two Variables
- Introduction to linear equations in two variables
- Graphical Method
- Substitution Method
- Elimination Method
- Cross - Multiplication Method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Consistency of Pair of Linear Equations
- Inconsistency of Pair of Linear Equations
- Algebraic Conditions for Number of Solutions
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Relation Between Co-efficient
Quadratic Equations
- Quadratic Equations
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Nature of Roots of a Quadratic Equation
- Relationship Between Discriminant and Nature of Roots
- Situational Problems Based on Quadratic Equations Related to Day to Day Activities to Be Incorporated
- Application of Quadratic Equation
Arithmetic Progressions
Coordinate Geometry
Lines (In Two-dimensions)
Constructions
- Division of a Line Segment
- Construction of Tangents to a Circle
- Constructions Examples and Solutions
Geometry
Triangles
- Similar Figures
- Similarity of Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Right-angled Triangles and Pythagoras Property
- Similarity of Triangles
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Triangles Examples and Solutions
- Concept of Angle Bisector
- Similarity of Triangles
- Ratio of Sides of Triangle
Circles
Trigonometry
Introduction to Trigonometry
- Trigonometry
- Trigonometry
- Trigonometric Ratios
- Trigonometric Ratios and Its Reciprocal
- Trigonometric Ratios of Some Special Angles
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
- Proof of Existence
- Relationships Between the Ratios
Trigonometric Identities
Some Applications of Trigonometry
Mensuration
Areas Related to Circles
- Perimeter and Area of a Circle - A Review
- Areas of Sector and Segment of a Circle
- Areas of Combinations of Plane Figures
- Circumference of a Circle
- Area of Circle
Surface Areas and Volumes
- Surface Area of a Combination of Solids
- Volume of a Combination of Solids
- Conversion of Solid from One Shape to Another
- Frustum of a Cone
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Different Combination of Solid Figures
- Surface Area and Volume of Three Dimensional Figures
Statistics and Probability
Statistics
Probability
Internal Assessment
Theorem - The Length of Two Tangent Segments Drawn from a Point Outside the Circle Are Equal
Notes
A circle can have atmost two parallel tangents.
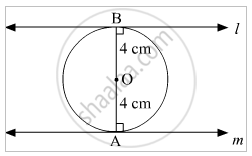
l and m are two tangents, radii OA and OB are ⊥ m and l respectively. As studied in 9th class, if the sum of co-interior angles between two lines is `180°` then the lines are parallel.
The point at which tangent touches a circle is known as point of contact. Here, point A and B are points of contact.
Only two tangents can be drawn from any external point of a circle.

The length of the segment of the tangent from the external point P and the point of contact with the circle is called the length of the tangent from the point P to the circle.
The lengths PT1 and PT2 are equal, this we will learn in the further concepts.
Theorem
Theorem- The lengths of tangents drawn from an external point to a circle are equal.
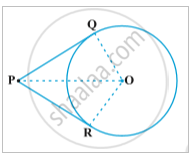
Given: A circle C (o,r) and an external point P. PQ and PR are lengths of circle.
To prove: PQ=PR
Proof: In ΔPOQ and ΔPOR
∠PRO and ∠PQO are right angled triangles (Theorem 1)
OQ = OR (Radii of the same circle)
Therefore, ∆ OQP ≅ ∆ ORP (Two right triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and the corresponding side of the other triangle.)
This gives PQ = PR (CPCT)