Graphical Representation of Cumulative Frequency Distribution

Topics

Number Systems
Real Numbers
- Introduction of Real Numbers
- Real Numbers Examples and Solutions
- Euclid’s Division Lemma
- Fundamental Theorem of Arithmetic
- Fundamental Theorem of Arithmetic Motivating Through Examples
- Proofs of Irrationality
- Concept of Irrational Numbers
- Rational Numbers and Their Decimal Expansions
Algebra
Polynomials
- Geometrical Meaning of the Zeroes of a Polynomial
- Relationship Between Zeroes and Coefficients of a Polynomial
- Division Algorithm for Polynomials
- Polynomials
Pair of Linear Equations in Two Variables
- Introduction to linear equations in two variables
- Graphical Method
- Substitution Method
- Elimination Method
- Cross - Multiplication Method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Consistency of Pair of Linear Equations
- Inconsistency of Pair of Linear Equations
- Algebraic Conditions for Number of Solutions
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Relation Between Co-efficient
Quadratic Equations
- Quadratic Equations
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Nature of Roots of a Quadratic Equation
- Relationship Between Discriminant and Nature of Roots
- Situational Problems Based on Quadratic Equations Related to Day to Day Activities to Be Incorporated
- Application of Quadratic Equation
Arithmetic Progressions
- Arithmetic Progression
- General Term of an Arithmetic Progression
- nth Term of an AP
- Sum of First ‘n’ Terms of an Arithmetic Progressions
- Derivation of the n th Term
- Application in Solving Daily Life Problems
- Arithmetic Progressions Examples and Solutions
Coordinate Geometry
Lines (In Two-dimensions)
- Coordinate Geometry
- Coordinate Geometry
- Distance Formula
- Section Formula
- Area of a Triangle
- Graphs of Linear Equations
- Basic Geometric Constructions
Constructions
- Division of a Line Segment
- Construction of Tangents to a Circle
- Constructions Examples and Solutions
Geometry
Triangles
- Similar Figures
- Similarity of Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Right-angled Triangles and Pythagoras Property
- Similarity of Triangles
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Triangles Examples and Solutions
- Concept of Angle Bisector
- Similarity of Triangles
- Ratio of Sides of Triangle
Circles
- Concept of Circle
- Tangent to a Circle
- Number of Tangents from a Point on a Circle
Trigonometry
Introduction to Trigonometry
- Trigonometry
- Trigonometry
- Trigonometric Ratios
- Trigonometric Ratios and Its Reciprocal
- Trigonometric Ratios of Some Special Angles
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
- Proof of Existence
- Relationships Between the Ratios
Trigonometric Identities
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
Some Applications of Trigonometry
- Heights and Distances
Mensuration
Areas Related to Circles
- Perimeter and Area of a Circle - A Review
- Areas of Sector and Segment of a Circle
- Areas of Combinations of Plane Figures
- Circumference of a Circle
- Area of Circle
Surface Areas and Volumes
- Surface Area of a Combination of Solids
- Volume of a Combination of Solids
- Conversion of Solid from One Shape to Another
- Frustum of a Cone
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Different Combination of Solid Figures
- Surface Area and Volume of Three Dimensional Figures
Statistics and Probability
Statistics
- Concepts of Statistics
- Mean of Grouped Data
- Mode of Grouped Data
- Median of Grouped Data
- Graphical Representation of Cumulative Frequency Distribution
- Concepts of Statistics
- Ogives (Cumulative Frequency Graphs)
Probability
- Basic Ideas of Probability
- Probability - A Theoretical Approach
- Sample Space
- Basic Ideas of Probability
- Concept Or Properties of Probability
- Simple Problems on Single Events
Internal Assessment

Notes

In this concept we will study about Relation of Ogive and Median. These graphical representation of the frequency distribution are called Ogives. Actual limits are on the x-axis and cumulative frequencies on the y-axis.

Ogive is also known as cumulative frequency distribution.

You will be asked to draw either a less than frequency ogive or more than frequency ogive.

Example: The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution :

Convert the distribution above to a less than type cumulative frequency distribution and also to a more than type cumulative frequency distribution, and draw its ogive.

1) Less than type cumulative frequency table

Classes	cf
Less than 10	2
Less than 15	14
Less than 20	16
Less than 25	20
Less than 30	23
Less than 35	27
Less than 40	30

2) More than type cumulative frequency table

Classes	cf
More than 5	30
More than 10	28
More than 15	16
More than 20	14
More than 25	10
More than 30	7
More than 35	3

The graphical representation of both the ogives will be

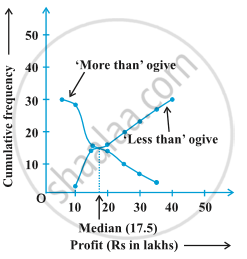
Here, $\frac{N}{2} = \frac{30}{2} = 15$

Now, we will take 15 on y axis and draw a perpendicular line that touches the curve, and from the point where the perpendicular touches the curve draw a perpendicular that touches the x axis, the point at which the perpendicular touches the x axis is the median.

Thus, here the Median is 17.5

If you would like to contribute notes or other learning material, please submit them using the button below.

Related QuestionsVIEW ALL [54]

The following is the distribution of weights (in kg) of 40 persons:

Weight (in kg)	40 – 45	45 – 50	50 – 55	55 – 60	60 – 65	65 – 70	70 – 75	75 – 80
Number of persons	4	4	13	5	6	5	2	1

Construct a cumulative frequency distribution (of the less than type) table for the data above.

Calculate the missing frequency form the following distribution, it being given that the median of the distribution is 24

Age (in years)	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
Number of persons	5	25	?	18	7

The monthly consumption of electricity (in units) of some families of a locality is given in the following frequency distribution:

Monthly Consumption (in units)	140 – 160	160 – 180	180 – 200	200 – 220	220 – 240	240 – 260	260 - 280
Number of Families	3	8	15	40	50	30	10

Prepare a ‘more than type’ ogive for the given frequency distribution.

For a frequency distribution, mean, median and mode are connected by the relation

In the formula $\bar{x} = a + h (\frac{\sum f_{i} u_{i}}{\sum f_{i}})$ , for finding the mean of grouped frequency distribution u_i = ______.

Change the following distribution to a 'more than type' distribution. Hence draw the 'more than type' ogive for this distribution.

Class interval:	20−30	30−40	40−50	50−60	60−70	70−80	80−90
Frequency:	10	8	12	24	6	25	15

If $u_{i} = \frac{x_{i} - 25}{10}, Σ f_{i} u_{i} = 20, Σ f_{i} = 100, then$ $\bar{X}$

If the median of the following frequency distribution is 32.5. Find the values of f₁ and f_2.

Graphical Representation of Cumulative Frequency Distribution

Advertisements

Topics

Number Systems

Real Numbers

Algebra

Polynomials

Pair of Linear Equations in Two Variables

Quadratic Equations

Arithmetic Progressions

Coordinate Geometry

Lines (In Two-dimensions)

Constructions

Geometry

Triangles

Circles

Trigonometry

Introduction to Trigonometry

Trigonometric Identities

Some Applications of Trigonometry

Mensuration

Areas Related to Circles

Surface Areas and Volumes

Statistics and Probability

Statistics

Probability

Internal Assessment

Notes

Related QuestionsVIEW ALL [54]

Advertisements

Submit content

Select a course