Trigonometric Ratios of Some Special Angles

1) Trignometric Ratios of 45°

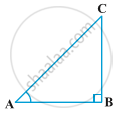
In ∆ ABC, right-angled at B, if one angle is 45°, then the other angle is also 45°, i.e., ∠ A = ∠ C = 45°

If two angles are equal then the sides opposite to them are also equal

therefore, BC = AB

Now, Suppose BC = AB = a.

Then by Pythagoras Theorem, `"AC"^2 = "AB"^2 + "BC"^2` = `a^2 + a^2 = 2a^2`,

and, therefore, AC = `asqrt2`.

Using the definitions of the trigonometric ratios, we have :

sin45°=`"perpendicular"/ "hypotenuse"`= `"BC"/"AC"`=`a/(asqrt2)` = `1/sqrt2`

cos45°= `"base"/ "hypotenuse"`= `"AB"/"AC"`= `a/ (asqrt2)` = `1/sqrt2`

tan45°= `"perpendicular"/"base"`= `"BC"/"AB"`= `a/a`= 1

Also, cosec 45° = `1/(sin45°)`= `sqrt2`,

sec 45° = `1/(cos45°)= sqrt2,`

cot 45° = `1/(tan45°) = 1.`

2)Trigonometric Ratios of 30° and 60°

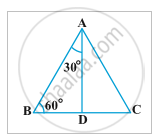
Let us now calculate the trigonometric ratios of 30° and 60°. Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore, ∠ A = ∠ B = ∠ C = 60°.

Draw the perpendicular AD from A to the side BC

AD is the common side in ∆ ABD and ∆ ACD

∆ ABD ≅ ∆ ACD (Angle-Side-Angle rule)

Therefore, BD = DC

and ∠ BAD = ∠ CAD (corresponding parts of congruent triangles)

∆ ABD is a right triangle, right-angled at D with ∠ BAD = 30° and ∠ ABD = 60°

let us suppose that AB = 2a.

Then, `BD =1/2"BC"= a`

`"AB"^2= "AD"^2+"BD"^2`

`2a^2= "AD"^2+ a^2`

`4a^2= "AD"^2+a^2`

`"AD"^2= 3a^2`

`"AD"= asqrt3`

Now, we have,

`sin 30°= "BD"/"AB"= a/(2a)= 1/2`,

`cos 30°= "AD"/"AB"= (asqrt3)/(2a)= sqrt3/2,`

`tan30°= "BD"/"AD"= a/(asqrt3)= 1/sqrt3,`

Also, `cosec  30°= 1/(sin30°)=2,`

`sec30°= 1/(cos30°)= 2/sqrt3` and

`cot30°= 1/(tan30°)`= `sqrt3`

Similarly, sin60°= `"AD"/"AB"= (asqrt3)/(2a)= sqrt3/2,`

cos60°= `1/2,`

tan60°= `sqrt3,`

cosec60°= `2/sqrt3,`

sec60°=2

and cot60°= `1/sqrt3`.

3) Trigonometric Ratios of 0°-

Let us see what happens to the trigonometric ratios of angle A, if it is made smaller and smaller in the right triangle ABC, till it becomes zero. As ∠ A gets smaller and smaller, the length of the side BC decreases. The point C gets closer to point B, and finally when ∠ A becomes very close to 0°, AC becomes almost the same as AB.

BC=0 and AC=AB

sin0°= `"BC"/"AC"= 0/"AC"= 0,`

cos0°= `"AB"/"AC"= 1`,

tan0°= `"BC"/"AB"= 0/"AB"= 0`,

cot0°= `1/(tan0°)`= not defined,

sec0°= `1/(cos0°)`= 1

and cosec0°= `1/(sin0°)`= not defined.

4)Trigonometric Ratios of 90°-

Now, let us see what happens to the trigonometric ratios of ∠ A, when it is made larger and larger in ∆ ABC till it becomes 90°. As ∠ A gets larger and larger, ∠ C gets smaller and smaller. Therefore, as in the case above, the length of the side AB goes on decreasing. The point A gets closer to point B. Finally when ∠ A is very close to 90°, ∠ C becomes very close to 0° and the side AC almost coincides with side BC.

AB=0 and AC=BC

sin90°= `"BC"/"AC"= 1`,

cos90°= `"AB"/"AC"= 0/"AC"= 0,`

tan90°= `"BC"/"AB"= "BC"/0`= not defined,

cot90°= `"AB"/"BC"= 0/"BC"= 0`,

sec90°= `"AC"/"AB"= "AC"/0`= not defined

and cosec90°= `"AC"/"BC"= 1.`

Let's sum up this information in a table,