Advertisements
Advertisements
Question
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
cosec 54° + sin 72°
Solution
We know `sin(90^@ - theta) = cos theta` and `cosec(90^@ - theta) = sec theta` So
`cosec 54° + sin 72° = cosec(90^@ - 36^@) + sin (90^@ - 18^@)`
`= sec 36^@ + cos 18^@`
hus the desired expression is sec 36^@ + cos 18^@`
APPEARS IN
RELATED QUESTIONS
Evaluate the following in the simplest form:
sin 60° cos 30° + cos 60° sin 30°
Evaluate the following:
`(sin 30° + tan 45° – cosec 60°)/(sec 30° + cos 60° + cot 45°)`
Evaluate the following :
(sin 72° + cos 18°) (sin 72° − cos 18°)
prove that:
tan (2 x 30°) = `(2 tan 30°)/(1– tan^2 30°)`
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratio: cos 45°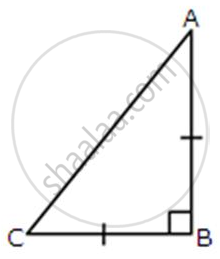
secθ . Cot θ= cosecθ ; write true or false
For any angle θ, state the value of: sin2 θ + cos2 θ
If A = B = 45° ,
show that:
cos (A + B) = cos A cos B - sin A sin B
Without using tables, evaluate the following: sec30° cosec60° + cos60° sin30°.
If A = 30° and B = 60°, verify that: `(sin("A" + "B"))/(cos"A" . cos"B")` = tanA + tanB
