Advertisements
Advertisements
Question
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
cot 85° + cos 75°
Solution
We know that `cot (90^@ - theta) = tan theta` and `cos (90^@ - theta) = sin theta` so
`cot 85° + cos 75° = cot(90^@ - 5^@) + cos(90^@ - 15^@)`
`= tan 5^@ +sin 15^@`
Thus the desired expression is `tan 56^@ + sin 15^@`
APPEARS IN
RELATED QUESTIONS
Find the value of x in the following :
tan 3x = sin 45º cos 45º + sin 30º
If x = 30°, verify that
(i) `\tan 2x=\frac{2\tan x}{1-\tan ^{2}x`
(ii) `\sin x=\sqrt{\frac{1-\cos 2x}{2}}`
Evaluate the following:
2tan2 45° + cos2 30° − sin2 60°
`(2 tan 30°)/(1-tan^2 30°)` = ______.
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
tan 65° + cot 49°
If sin x = cos y, then x + y = 45° ; write true of false
find the value of: cos2 60° + sin2 30°
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratio: cos 45°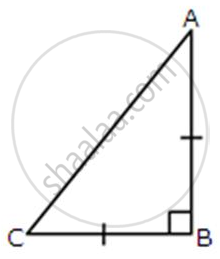
If A = B = 45° ,
show that:
cos (A + B) = cos A cos B - sin A sin B
If sin 30° = x and cos 60° = y, then x2 + y2 is
