notes
Here what will be the distance between points PQ? To find this we will use distance formula.
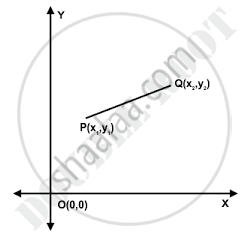
Distance formula says, PQ= `sqrt[ (x_2-x_1)^2 + (y_2-y_1)^2]`
Example1- Find the distance between the points P(6,-6) and O(0,0)
Solution: `x_2=0, x_1=6, y_2=0 and y_1=-6`
PO= `sqrt[ (x_2-x_1)^2 + (y_2-y_1)^2]`
= `sqrt[ (0-6)^2 + (0+6)^2]`
= `sqrt[ (-6)^2 + (6)^2]`
= `sqrt[ 36+36]`
= `sqrt72`
PO = 6 `sqrt2` units
Example2- Find the values of x for which the distance between the points P(4,-5) and Q(12,x) is 10 units
Solution: PQ=10
`x_2= 12, x_1=4, y_2=x and y_1=-5`
PQ= `sqrt[ (x_2-x_1)^2 + (y_2-y_1)^2]`
10 = `sqrt[ (12-4)^2 + (x+5)^2]`
= `sqrt[ (8)^2 + (x+5)^2]`
= `sqrt[ 64 + (x+5)^2]`
Sqauring both the sides
`100= 64+ (x+5)^2`
`36= (x+5)^2`
`+or-6 = x+5`
`x= 6-5 or x= -6-5`
`x=1 or x= -11`
Example3- Find the point P on x-axis which is equidistance from the points A(5,-2) and B(-3,2)
Solution: Let the point be P(x,0)
Now, PA=PB [Given as point P on x-axis is equidistance from the points A(5,-2) and B(-3,2)]
`"PA"^2="PB"^2`
`(x_2-x_1)^2 + (y_2-y_1)^2 = (x_2-x_1)^2 + (y_2-y_1)^2`
`(5-x)^2 + (-2-0)^2 = (-3-x)^2 + (2-0)^2`
`25+x^2-10x+4 = (-3)^2 +x^2 -2(-3)(x) +4`
`25+x^2-10x+4 = 9+x^2+6x+4`
`16x= 16`
`x=1`
Therefore, point P is (1,0)
