Advertisements
Advertisements
Question
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

Solution
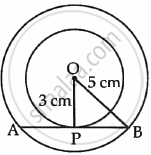
Given that,
Radius of smaller circle = 3 cm
Radius of larger circle = 5 cm
In triangle, OPB
`\implies` (OB)2 = (OP)2 + (BP)2
`\implies` (5)2 = (3)2 + (BP)2
`\implies` (BP)2 = 25 – 9 = 16 = (4)2
`\implies` BP = 4 cm
Also, AP = BP ...(As tangent is bisected at the point of contact)
So, AP = BP = 4 cm
`\implies` AB = 4 + 4 = 8 cm
Length of chord AB = 8 cm.
RELATED QUESTIONS
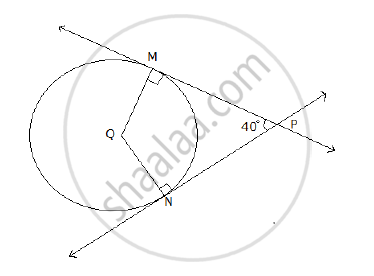
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19 ?
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

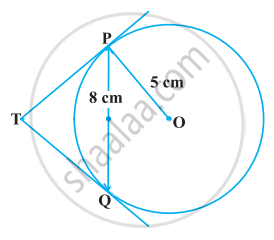
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
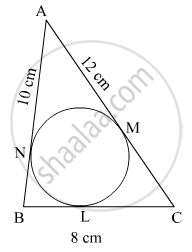
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
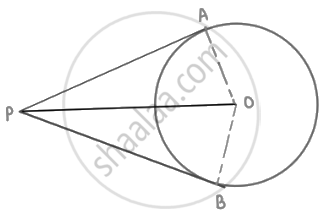
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

