Advertisements
Advertisements
Question
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

Solution
ABCD is a parallelogram.
∴ AB = CD .....(1) (Opposite sides of parallelogram are equal)
AD = BC .....(2) (Opposite sides of parallelogram are equal)
Tangent segments drawn from an external point to a circle are congruent.
AE = AH .....(3)
DG = DH .....(4)
BE = BF .....(5)
CG = CF .....(6)
Adding (3), (4), (5) and (6), we get
AE + BE + CG + DG = AH + DH + BF + CF
⇒ AB + CD = AD + BC .....(7)
From (1), (2) and (7), we have
2AB = 2AD
⇒ AB = AD
∴ AD = AB = AE + EB = 4.5 + 5.5 = 10 units
APPEARS IN
RELATED QUESTIONS
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
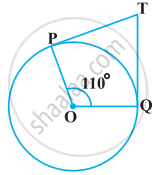
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
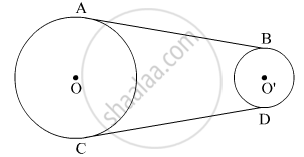
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
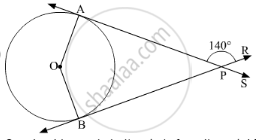
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19 ?
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
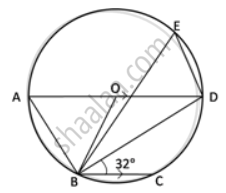
Find: ∠BED
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
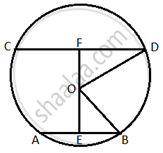
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
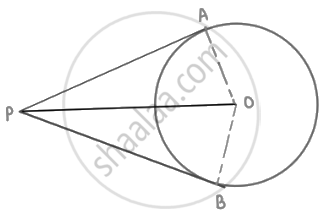
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
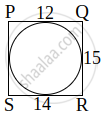
A quadrilateral PQRS is drawn to circumscribe a circle. If PQ = 12 cm, QR = 15 cm and RS = 14 cm, then find the length of SP is ______.