Advertisements
Advertisements
Question
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
Solution
Draw a circle with centre O and take an external point P.
PA and PB are the tangents.
Join OP.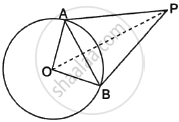
Now in ΔOAP and ΔOBP,
OA = OB ...(Radius of circle)
OP = OP ...(Common)
PA = PB ...(Tangents are equal)
So, by S.S.S criteria,
ΔOAP ≅ ΔOBP
So, ∠APO = ∠BPO
Hence, OP bisects ∠APB.
APPEARS IN
RELATED QUESTIONS
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

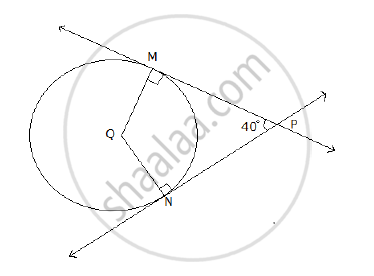
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Find the area of the shaded region in Fig. 8, where \\

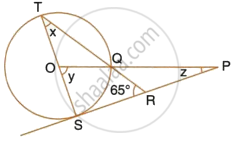
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
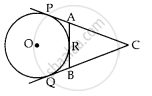
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______
The length of the tangent from an external point P on a circle with centre O is ______
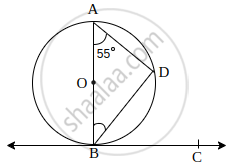
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
