Advertisements
Advertisements
Question
Find the area of the shaded region in Fig. 8, where \\

Solution
Area of the shaded region
= Area of the semicircle with diameter AD + Area of the semicircle with diameter BC
− Area of the semicircle with diameter AB − Area of the semicircle with diameter CD
\[= \frac{1}{2}\pi \left( \frac{14}{2} \right)^2 + \frac{1}{2}\pi \left( \frac{7}{2} \right)^2 - \frac{1}{2}\pi \left( \frac{3 . 5}{2} \right)^2 - \frac{1}{2}\pi \left( \frac{3 . 5}{2} \right)^2 \]
\[ = \frac{1}{2} \times \frac{22}{7} \times \left( \frac{3 . 5}{2} \right)^2 \times \left[ 16 + 4 - 1 - 1 \right]\]
\[ = \frac{1}{2} \times \frac{22}{7} \times \frac{3 . 5}{2} \times \frac{3 . 5}{2} \times 18\]
\[ = 86 . 625 {cm}^2\]
APPEARS IN
RELATED QUESTIONS
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19 ?
Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
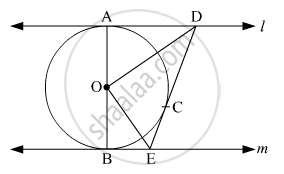
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
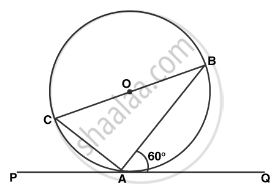
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
The length of tangent from an external point P on a circle with centre O is always less than OP.
