Advertisements
Advertisements
Question
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
Solution
AD is parallel to BC, i.e., AO is parallel to BC and OB is transversal.
⇒ ∠ AOB = ∠ OBC ......(Alternate angles)
⇒ ∠ OBC = ∠ OBD + ∠ DBC
⇒ ∠OBC = 32° + 32°
⇒ ∠OBC = 64°
⇒ ∠ AOB = 64°
APPEARS IN
RELATED QUESTIONS
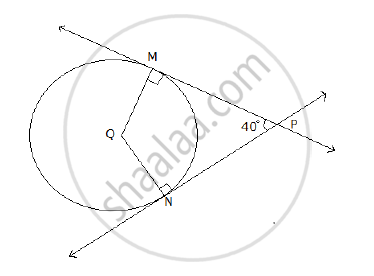
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Prove that a parallelogram circumscribing a circle is a rhombus.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.