Advertisements
Advertisements
Question
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
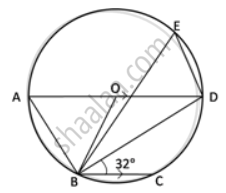
Find: ∠BED
Solution
In Δ OAB ,
OA = OB ...(Radii of the same circle° )
⇒ ∠ OAB = ∠ OBA = x (say)
⇒ ∠ OAB + ∠ OBA + ∠ AOB = 180°
⇒ x + x + 64° = 180°
⇒ 2x = 180 ° - 64 °
⇒ 2x = 116°
⇒ x = 58°
⇒ ∠ OAB = 58°
i.e. ∠ DAB = 58°
⇒ ∠ DAB = ∠BED = 58° ....(Angles inscribed in the same arc are equal)
APPEARS IN
RELATED QUESTIONS
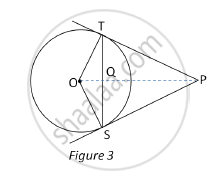
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
The number of tangents drawn at a point of the circle is/are ______
The length of the tangent from an external point on a circle is ______
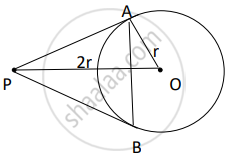
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

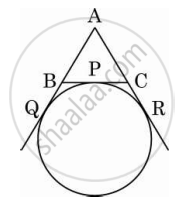
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).