Advertisements
Advertisements
Question
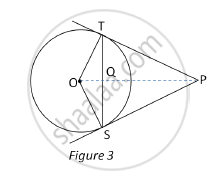
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
Solution
In the given figure,
OP = 2r … (Given)
∠OTP = 90° … (radius drawn at the point of contact is perpendicular to the tangent)
In OTP,
sin OPT =`(OT)/(OP)=1/2`= sin30°
⇒ ∠OPT=30°
∴ ∠TOP=60°
∴ ΔOTP is a 30°-60°-90°, right triangle.
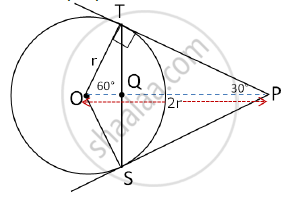
In ΔOTS,
OT = OS … (Radii of the same circle)
∴ ΔOTS is an isosceles triangle.
∴ ∠OTS = ∠OST … (Angles opposite to equal sides of an isosceles triangle are equal)
In ΔOTQ and ΔOSQ
OS = OT … (Radii of the same circle)
OQ = OQ ...(side common to both triangles)
∠OTQ = ∠OSQ … (angles opposite to equal sides of an isosceles triangle are equal)
∴ ΔOTQ ≅ ΔOSQ … (By S.A.S)
∴ ∠TOQ = ∠SOQ = 60° … (C.A.C.T)
∴ ∠TOS = 120° … (∠TOS = ∠TOQ + ∠SOQ = 60° + 60° = 120°)
∴ ∠OTS + ∠OST = 180° – 120° = 60°
∴ ∠OTS = ∠OST = 60° ÷ 2 = 30°
APPEARS IN
RELATED QUESTIONS
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that the lengths of the tangents drawn from an external point to a circle are equal.
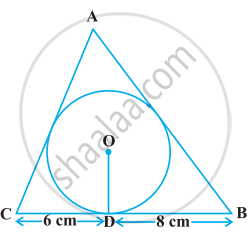
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see given figure). Find the sides AB and AC.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
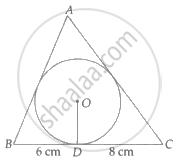
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
