Question

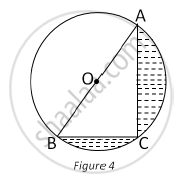
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)

Answer 1

Diameter, AB = 13 cm

∴ Radius of the circle, `r=13/2=6.5 cm`

∠ACB is the angle in the semi-circle.

∴ ∠ACB = 90°

Now, in ACB, using Pythagoras theorem, we have

AB²=AC²= BC²

∴ (13)²=(12)²+(BC)²

∴ (BC)² =(13)²-(12)²=169-144=25

∴ BC = `sqrt25=5cm`

Now, area of shaded region= Area of semi-circle- Are of ΔACB

`=1/2pir^2 -1/2xxBCxxAC`

`=1/2xx3.14xx(6.5)^2-1/2xx5xx12`

= 66.33-30

= 36.33 cm²

Thus, the area of the shaded region is 36.33 cm² .