Advertisements
Advertisements
प्रश्न
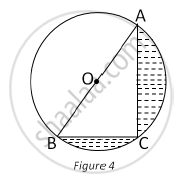
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
उत्तर
Diameter, AB = 13 cm
∴ Radius of the circle, `r=13/2=6.5 cm`
∠ACB is the angle in the semi-circle.
∴ ∠ACB = 90°
Now, in ACB, using Pythagoras theorem, we have
AB2=AC2= BC2
∴ (13)2=(12)2+(BC)2
∴ (BC)2 =(13)2-(12)2=169-144=25
∴ BC = `sqrt25=5cm`
Now, area of shaded region= Area of semi-circle- Are of ΔACB
`=1/2pir^2 -1/2xxBCxxAC`
`=1/2xx3.14xx(6.5)^2-1/2xx5xx12`
= 66.33-30
= 36.33 cm2
Thus, the area of the shaded region is 36.33 cm2 .
APPEARS IN
संबंधित प्रश्न
If the circumference of a circular sheet is 154 m, find its radius. Also find the area of
the sheet. (Take `pi = 22/7`)
Find the perimeter of a semicircular protractor whose diameter is 14 cm.
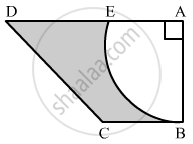
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then ______.
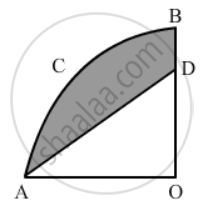
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm. find the area of
- quadrant OACB
- the shaded region.
The diameter of a cycle wheel is `4 5/11` cm. How many revolution will it make in moving 6.3 km ?
A conical tent requires 264 m2 of canvas. If the slant height is 12 m, find the vertical height of the cone.
A wire bent in the form of an equilateral triangle has an area of `121sqrt(3)"cm"^2`. If the same wire is bent into the form of a circle, find the area enclosed by the wire.
The circumference of a circle is equal to the perimeter of a square. The area of the square is 484 sq.m. Find the area of the circle.
Areas of two circles are equal. Is it necessary that their circumferences are equal? Why?
