Advertisements
Advertisements
Question
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

Solution
In a cyclic quadrilateral ABCD,
`∠ ABC+∠ADC=180°` (Opposite angle of a cydic quadrilateral are supplementary)
`⇒ 100°+∠ADC=180°`
`⇒ ∠ADC=80°`
Now, in `ΔACD`,
`∠ADC+∠CAD+∠ADC=180°`
`⇒40°+∠CAD+80°=180°`
`⇒∠CAD=180°-120°`
`⇒∠CAD=60°`
`"Now" ∠DCT=∠CAD ...........("angles in the alternate segment are equal")`
`∴ ∠DCT=60°`
APPEARS IN
RELATED QUESTIONS
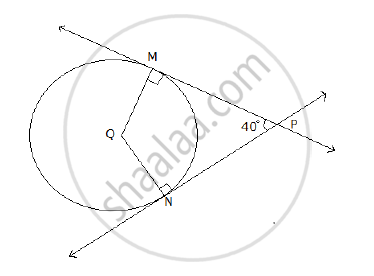
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
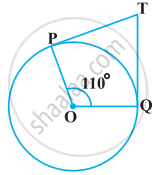
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
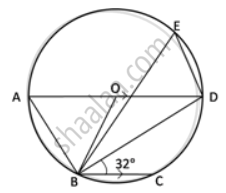
Find: ∠BED
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
The length of the tangent from an external point on a circle is ______
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

