Advertisements
Advertisements
Question
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
Solution
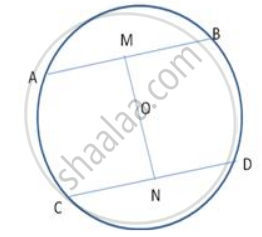
AM = MB
CN = ND
∴ OM ⊥ AB
and ON ⊥ CD
(A line bisecting the chord and passing through the centre of the circle is perpendicular to the chord)
∴ ∠ OMA = ∠ OND = 90° each
But these are alternate interior angles
∴ AB || CD
APPEARS IN
RELATED QUESTIONS
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
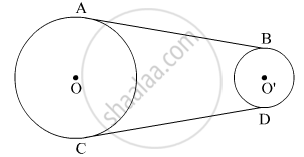
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
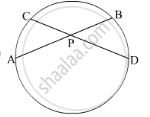
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
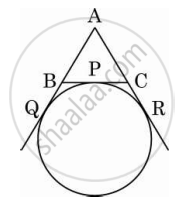
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).