Advertisements
Advertisements
Question
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Solution
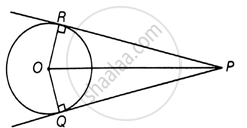
Given: Two tangents PQ and PR are drawn from an external point to a circle with centre O.
To Prove: QORP is a cyclic quadrilateral.
Proof: Since, PR and PQ are tangents.
So, OR ⊥ PR and OQ ⊥ PQ ...[Since, if we drawn a line from centre of a circle to its tangent line. Then, the line always perpendicular to the tangent line]
∴ ∠ORP = ∠OQP = 90°
Hence, ∠ORP + ∠OQP = 180°
So, QOPR is cyclic quadrilateral. ...[If sum of opposite angles is quadrilateral in 180°, then the quadrilateral is cyclic]
Hence proved.
APPEARS IN
RELATED QUESTIONS
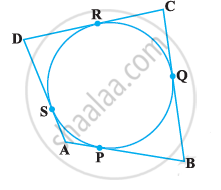
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
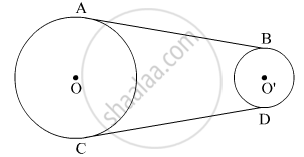
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
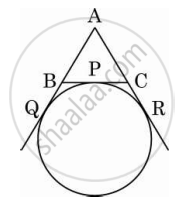
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

