Advertisements
Advertisements
Question
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Solution
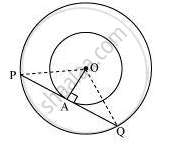
Let the two concentric circles be centered at point O.
Also, a > b where a is the radius of a larger circle and b is the radius of the smaller circle.
And let PQ be the chord of the larger circle which touches the smaller circle at point A. Therefore, PQ is tangent to the smaller circle.
OA ⊥ PQ (As OA is the radius of the circle)
Applying Pythagoras theorem in ΔOAP, we obtain
OA2+AP2=OP2
b2 + PA2 = a2
⇒ PA2 = a2 - b2
⇒ PA =
In ΔOPQ,
Since OA ⊥ PQ,
PA = AQ (Perpendicular from the center of the circle to the chord bisects the chord)
∴ PQ =2PA =
Therefore, the length of the chord of the larger circle is
APPEARS IN
RELATED QUESTIONS
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
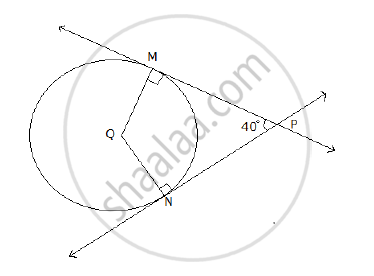
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
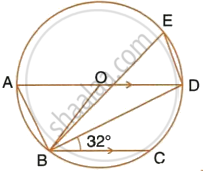
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
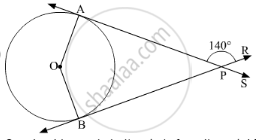
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
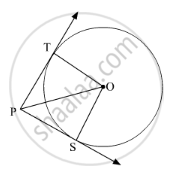
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of the tangent from an external point P on a circle with centre O is ______
The angle between two tangents to a circle may be 0°.
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

